Kevesen tudják, hogy az amatőrcsillagászok között leginkább elterjedt kritérium az optikák minőségének jellemzésére valójában könnyen félrevezető lehet. Ideje, hogy „leszámoljunk” a megszokott P-V értékekkel és olyan mutatót használjunk, amely sokkal inkább jellemzi a távcső optikai minőségét. Ez pedig a Strehl-érték, melynek számítása nem új keletű, bár sokak számára talán kevéssé ismert fogalom volt eddig.
A Strehl érték annyira könnyen érthető mint a megszokott P-V érték, mégis sokkal pontosabb és átfogóbb képet ad a távcső optikai minőségéről. Noha számítása a gyakorlatban bonyolult, az értelmezése meglehetősen egyszerű.
A P-V érték
Az alábbi ábra jól jellemzi a P-V számítás gyengeségét. Mindkettő egy-egy Newton távcső főtükrének keresztmetszetét mutatja meg, pontosságuk lambda/10 P-V, röviden L/10 P-V. Ez nem jelent más, mint a legnagyobb „hullámhegy” és „hullámvölgy” közötti eltérés, legfeljebb a fény hullámhosszának (lambda) 1/10-e. Ennek ellenére a tükrök felülete meglehetősen eltérő. Első pillantásra – mindenféle kifinomult analízis nélkül – melyik tükröt szeretné megvásárolni?

A válasz elég nyilvánvaló, akár csak az is, hogy a P-V érték önmagában miért nem kellően pontos az optika jellemzésére. Csak a legnagyobb eltérés értékét adja meg, más fontos jellemző, mint a felület „érdessége”, kimarad a számításból. Látható az is, hogy egy-egy kis felületre jellemző nagyobb eltérés (pl. karc) látszólag teljesen „elrontja” az optika minőségét, noha az a gyakorlatban nem okoz számottevő képminőség-romlást. Ennek ismeretében érthető, hogy egy L/2 P-V pontosságú tükör akár egy kimagaslóan jó optika is lehet, amennyiben felületének nagy részén az eltérések pl. L/10 P-V alatt maradnak.
Érdemes megemlíteni, lényeges jellemző, hogy a fenti érték a hullámhegy és a hullámvölgy közötti különbségre utal. (Ezt jelzi a P-V- peak-to-valley – szócska.) Amennyiben a fenti optika esetében felületi pontosságot adunk meg – azaz a legnagyobb hullámhegy vagy -völgy méretét az ideális felszínhez képest számoljuk -, akkor az értékek feleződnek, tehát a felület pontossága L/20. Képzeljük el a Balaton vizét, amikor nyugalomban van. Ha ehhez képest a legnagyobb hullámhegy és -völgy külön-külön 1 m, akkor a hullámhegy és -völgy távolsága 2 m.
Az RMS érték
Az RMS szintén az optikai felületek minőségét jellemzi, a P-V értéknél azonban sokkal pontosabban. Ennek meghatározása során a felület több pontján veszünk mintát, majd ezek alapján határozzuk meg annak pontosságát. Amint látható, ez az érték a teljes felületet jellemzi, csökkentve azon kis részek jelentőségét, melyek az „átlagos” minőségtől eltérnek.
Számolása meglehetősen összetett művelet, a részletekbe emiatt nem bocsátkozunk. Sokkal fontosabb ennél azt tudni, hogy a közismert P-V értékekhez hogyan viszonyul. Marechal számításai szerint RMS 0.071 esetén tekinthető egy optikai diffrakció határoltnak, vagyis ez az érték felel meg a közismert L/4 P-V-nek.
A Strehl érték
Az RMS érték tehát P-V értéknél pontosabban utal egy távcső optikájának minőségére, azonban egy átlag amatőr számára kevéssé szemléletes mutató. Az RMS értékből egyszerűen kiszámítható a Strehl-érték, mely ugyanolyan pontosan, ám sokkal közérthetőbben jellemzi mennyire áll közel egy adott távcső teljesítőképessége a típustól elvárható maximálishoz.
A Strehl egyik legnagyobb előnye, hogy az optika teljesítőképességét az elméletileg elérhetőhöz viszonyítja, s nem felületének pontosságát jellemzi. Nagyon egyszerűen megfogalmazva: megmutatja, hogy a bejövő fény hány százaléka kerül az Airy-korongba az ideális optikához képest. Leggyakrabban 0 és 1 közé eső számmal, ritkábban százalékban kifejezve adják meg. A tökéletes rendszer esetében ez az érték 1, tehát a Strehl 0.95 azt jelenti, hogy az optikától ideális esetben elvárható értékhez képest a fény 95%-a kerül az Airy korongba, míg 5% az azt körbevevő gyűrűkbe (azok közül is leginkább az elsőbe) csökkentve a kontrasztot.
Ezen a ponton a (máshonnan már tájékozott) olvasóban felmerülhet a kérdés: ha egy tökéletes, központi kitakarás nélküli optika esetében a fény „mindössze” 84%-a kerül az Airy korongba, míg a központi kitakarással rendelkező rendszerek esetében kevesebb, hogyan érhető el 1-hez közeli Strehl érték?! A válasz egyszerű és korábban már említettük is: 1-nek – a kitakarás mértékétől függetlenül – az adott rendszer tökéletes optikával rendelkező „változata” tekintendő.
Amint látható a mutató meglehetősen egyszerűen jellemzi a távcső optikai minőségét, de mik az elvárható értékek? 0.8 elég? Vagy legyen 0.9 esetleg 0.95? És ezek az értékek hogyan viszonyulnak – még ha hozzávetőlegesen is – a közismert P-V értékekhez?
Az alábbi táblázat választ ad a fenti kérdésekre.
|
Felületi pontosság a különböző mutatókkal kifejezve (550 nm-en értékelve) |
|||
| P-V | Marechal RMS | Strehl érték | Megjegyzés |
| 1/3 | 0.094 | 0.71 | |
| 1/4 | 0.071 | 0.82 | Diffrakció-határolt |
| 1/5 | 0.057 | 0.88 | |
| 1/6 | 0.047 | 0.92 | Jó |
| 1/7 | 0.041 | 0.94 | Nagyon jó |
| 1/8 | 0.036 | 0.95 | Kitűnő |
| 1/9 | 0.032 | 0.960 | Kitűnő |
| 1/10 | 0.028 | 0.969 | Kitűnő |
| 1/11 | 0.026 | 0.974 | |
| 1/12 | 0.024 | 0.978 | |
Végezetül szeretnénk néhány megjegyzést fűzni a táblázathoz: érdemes szem előtt tartani, hogy a megadott értékek az elérhető teljesítmény maximumát jelentik. A gyakorlatban egy optika sosem éri el azt a szintet, leginkább a légköri nyugtalanság miatt, de a kollimációs hibák és a fényútban levő egyéb optikai elemek is rontják a képminőséget.
A fentiekben többször volt szó arról, hogy az optika pontosságát a fény hullámhosszának töredékében adjuk meg (pl. lambda/10). Ebből következően nem elhanyagolható paraméter a vizsgálatra használt fény hullámhossza (színe). Mivel a szem kb. 550 nm-es hullámhosszon (zöld szín) a legérzékenyebb ezért a méréseket célszerű ilyen fényben kiértékelni. Amennyiben a mérés más hullámhosszon történik, a kiértékelés során van lehetőség korrekcióra.
A leírásban alapvetően Newton távcsövek tükréről esett szó, melynek felületének pontossága könnyen elképzelhető lévén a fény egy felületről verődik vissza. De mi a helyzet a lencsés távcsövek esetében ahol objektívjüket nemritkán 3 lencsetag, azaz 6 felület alkotja? Hogyan tudjuk ezeknél a L/4 felületi hibát ártelmezni? A „titok nyitja”, hogy nem közvetlenül az optikai elemek felületének pontosságát kell elképzelni, hanem az általuk fókuszált fénysugarak által alkotott „felületét”. Szaknyelven szólva ez a hullámfront, vagyis a lencsétől/tükörtől azonos fázisban levő „fénysugarak” által létrehozott képzeletbeli „felület”. Amennyiben a lencse / tükör felülete eltér az ideálistól, az általa fókuszált „fénysugarak” azonos fázisban eltérő távolságban lesznek és ez az eltérés adja a korábban többször is említett felületi hibát.
Az alábbiakban két darab 150/750-es newton tükörről készült interferogramot mutatunk. A fenti ismeretek birtokában valószínűleg nem lesz nehéz eldönteni melyik sikerült jobban.
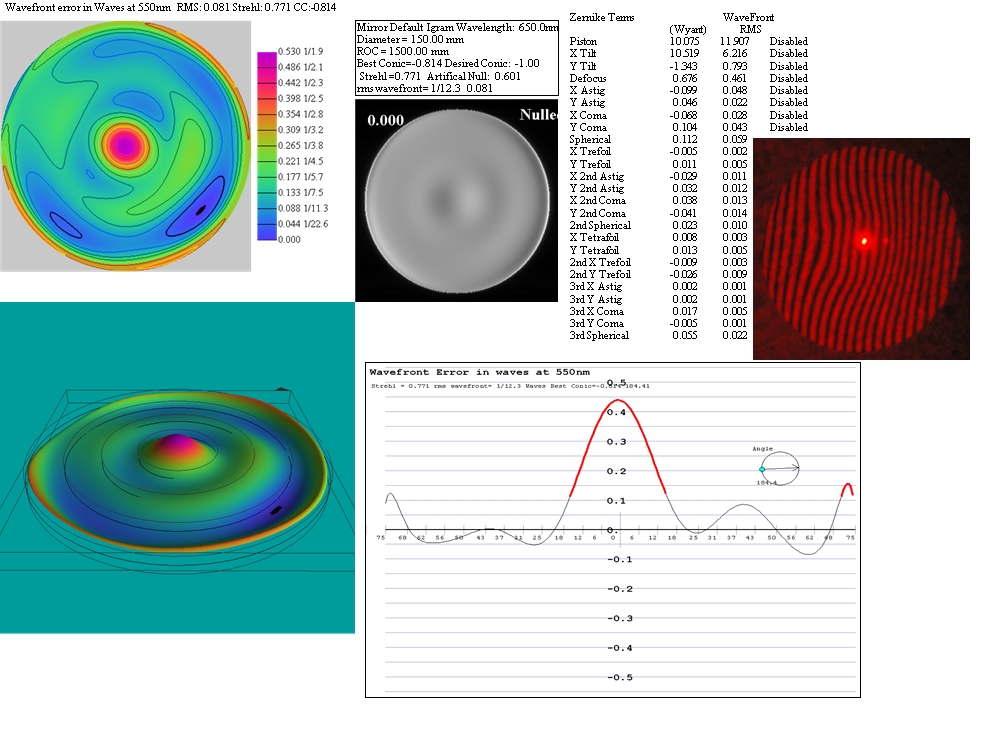 |
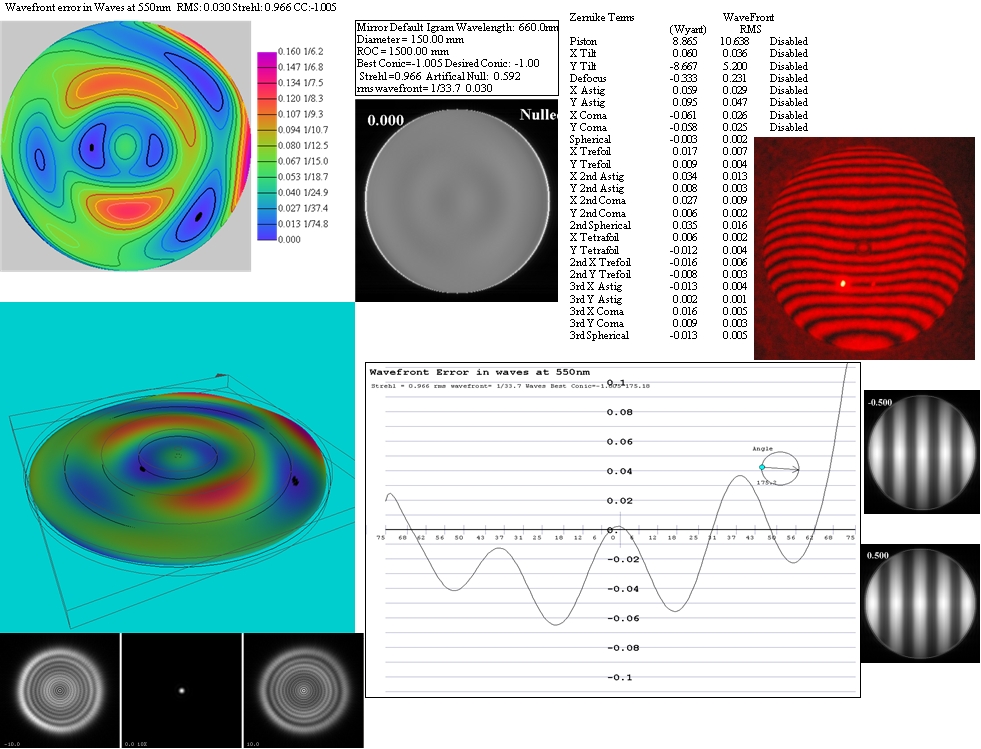 |
A cikk megírása során felhasználtuk R. F. Royce „A Better Method of Measuring Optical Performance” c. írását.
Kapcsolódó cikkek
Nincs további cikk.

